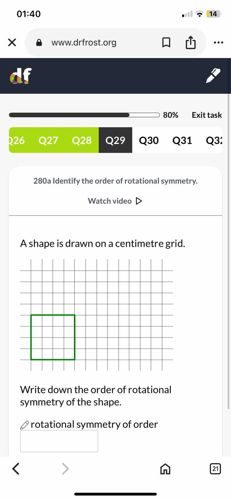
A shape is drawn on a centimetre grid. Write down the order of rotational symmetry of the shape. The shape drawn is a square.

Answer

The shape shown on the grid is a square. The order of rotational symmetry is the number of times a shape can be rotated by less than 360 degrees and still look the same as its original position. A square has four equal sides and four right angles. Let's consider rotating a square around its center: 1. After a 90-degree rotation, the square will look identical to its original position. 2. After a 180-degree rotation (two 90-degree turns), the square will again look identical to its original position. 3. After a 270-degree rotation (three 90-degree turns), the square will once more look identical to its original position. 4. After a 360-degree rotation, the square returns to its exact starting position, which is always counted as one instance for any shape, but the 'order' refers to distinct identical appearances within a full turn. Since the square looks identical to its original position at 90, 180, and 270 degrees (three distinct rotations less than 360 degrees, plus the initial position), the order of rotational symmetry is 4. Therefore, the rotational symmetry of order is 4.