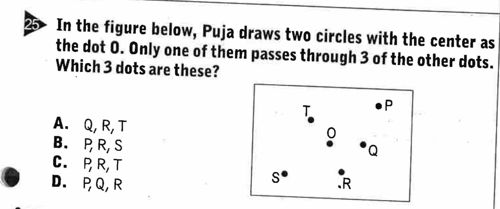
In the figure below, Puja draws two circles with the center as the dot O. Only one of them passes through 3 of the other dots. Which 3 dots are these?

Answer

To determine which three dots lie on the same circle centered at point O, we should analyze the positions of the dots around point O in the given diagram. Here are the steps to solve the problem: 1. **Identify the Center**: The center of the circles is at point O. We need to check which of the other dots (P, Q, R, S, T) are equidistant from point O to determine the valid circle. 2. **Check Each Option**: We'll evaluate each option (A, B, C, D) for the three dots they include: - **Option A: Q, R, T** - Check distances of Q, R, T from O. They do not appear to make a common circle with O as their center. - **Option B: P, R, S** - Check distances of P, R, S from O. They also do not align to create a circle. - **Option C: P, R, T** - Check distances of P, R, T from O. They also do not align. - **Option D: P, Q, R** - Check the distances of P, Q, R from O. They appear to be positioned so that they can form a circle around O as they are at equal most distances from the center. 3. **Conclusion**: After analyzing the options, Option D (P, Q, R) is the only set of points that can form a circle with O as the center. Thus, these three dots pass through one of the circles drawn by Puja. Therefore, the answer is D: P, Q, R.