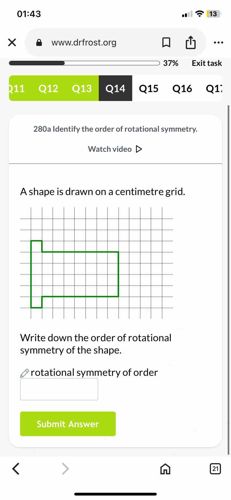
A shape is drawn on a centimetre grid. Write down the order of rotational symmetry of the shape.

Answer

The given shape consists of a rectangle with a smaller rectangle vertically attached to its left side, creating an 'F' like shape rotated 90 degrees clockwise or an 'L' like shape. To determine the order of rotational symmetry, we need to find how many times the shape looks identical as it is rotated 360 degrees around its center point. Let's analyze the shape: 1. At 0 degrees (its original position), the shape is clearly visible. 2. If we rotate the shape by 90 degrees clockwise, the 'extension' part that was on the left will now be on the top, and the main rectangular part will be reoriented. The shape will not look the same as the original. 3. If we rotate the shape by 180 degrees clockwise, the 'extension' part will be on the right side of the main rectangle, and it will be upside down relative to its original orientation. Again, the shape will not look the same as the original. 4. If we rotate the shape by 270 degrees clockwise, the 'extension' part will be on the bottom, and the main rectangle will also be reoriented. The shape will not look the same. 5. Finally, if we rotate the shape by 360 degrees clockwise, it returns to its original position. Since the shape only looks identical to its original form at 360 degrees (which is the same as 0 degrees), and not at any intermediate angles (like 90, 180, or 270 degrees), its order of rotational symmetry is 1. An object has an order of rotational symmetry of 1 if it only maps onto itself once in a full 360-degree rotation. Therefore, the order of rotational symmetry is 1.