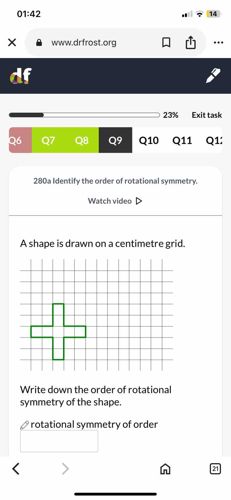
A shape is drawn on a centimetre grid. Write down the order of rotational symmetry of the shape.

Answer

The shape provided is a '+' (plus sign) shape. To find the order of rotational symmetry, we need to determine how many times the shape looks exactly the same when rotated 360 degrees around its central point. Let's consider rotating the given shape: 1. Initial position: The shape appears as shown. 2. Rotate 90 degrees clockwise: If you rotate the '+' shape by 90 degrees, it will still look exactly the same. 3. Rotate 180 degrees clockwise: Rotating it by another 90 degrees (total 180 degrees) will also make it look the same. 4. Rotate 270 degrees clockwise: Rotating it by yet another 90 degrees (total 270 degrees) will make it look the same. 5. Rotate 360 degrees clockwise: Rotating it by a final 90 degrees (total 360 degrees) brings it back to its original position, looking the same. Since the shape looks identical at 0 degrees (initial position), 90 degrees, 180 degrees, and 270 degrees during a full 360-degree rotation, it means it matches its original appearance 4 times. Therefore, the order of rotational symmetry is 4.