Solve the equation \(|-\frac{x}{6}| = 12\).

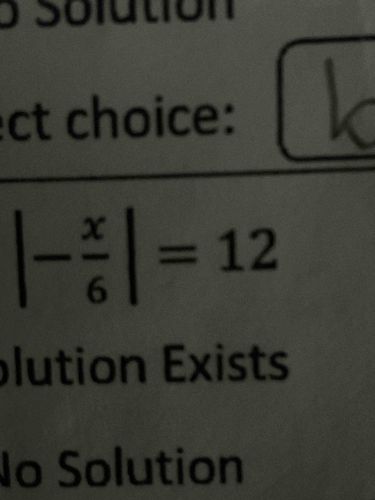
Answer

To solve the equation \(|-\frac{x}{6}| = 12\), we first recognize that the absolute value function, \(|a| = b\), implies two possible equations: \(a = b\) or \(a = -b\). 1. Starting with the given equation, we can rewrite it as: \[ -\frac{x}{6} = 12 \quad \text{or} \quad -\frac{x}{6} = -12 \] 2. Solving the first case, \(-\frac{x}{6} = 12\): - Multiply both sides by -1: \[ \frac{x}{6} = -12 \] - Now multiply both sides by 6: \[ x = -72 \] 3. Now, solving the second case, \(-\frac{x}{6} = -12\): - Multiply both sides by -1: \[ \frac{x}{6} = 12 \] - Multiply both sides by 6: \[ x = 72 \] 4. Therefore, the two solutions to the equation are: \[ x = -72 \quad \text{and} \quad x = 72 \] The final answer includes both solutions: \(x = -72\) and \(x = 72\).