A shape is drawn on a centimetre grid. Write down the order of rotational symmetry of the shape.

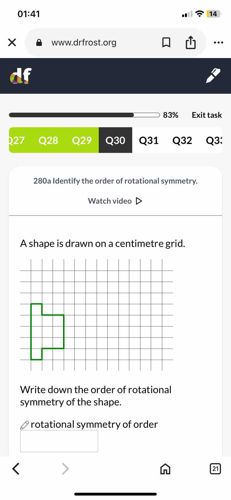
Answer

The order of rotational symmetry is the number of times a shape can be rotated about its center point and still look the same. For the given shape, let's analyze its rotational symmetry: 1. **Original Position:** The shape looks as shown. 2. **Rotation by 90 degrees (clockwise or counter-clockwise):** If you rotate the shape by 90 degrees, it will not look the same as the original. For example, the 'L' section will be in a different orientation relative to the 'stalk'. 3. **Rotation by 180 degrees:** If you rotate the shape by 180 degrees, it will also not look the same. The 'L' section will be on the opposite side of the 'stalk' in an inverted orientation relative to the original. 4. **Rotation by 270 degrees:** Similar to 90 degrees, it will not match the original. 5. **Rotation by 360 degrees:** After a full 360-degree rotation, the shape will return to its original position, obviously looking the same. This always counts as one instance of symmetry. Since the shape only looks the same as its original orientation after a full 360-degree rotation (i.e., returning to its starting position), it has an order of rotational symmetry of 1. Therefore, the order of rotational symmetry of the shape is 1.