What is the value of u in the given geometric problem involving angles?

Answer

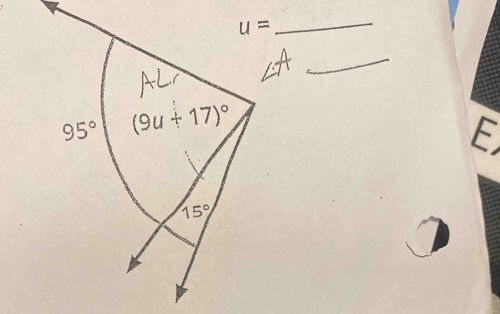
To find the value of u, we need to use the properties of angles. In the provided figure, we see two intersecting lines forming different angles. We know that the sum of the angles on a straight line is 180 degrees. 1. The angle at the top of the figure is given as 95 degrees. 2. There is another angle labeled as (9u + 17) degrees adjacent to the 95 degrees angle. 3. The angle at the bottom of the figure is given as 15 degrees. Setting up the equation: The angles along the straight line must sum to 180 degrees: 95 + (9u + 17) + 15 = 180 Now, we can simplify the equation: 95 + 17 + 15 equals 127 degrees. Substituting this into the equation: 127 + 9u = 180 Subtract 127 from both sides: 9u = 180 - 127 9u = 53 Now, divide both sides by 9 to isolate u: u = 53 / 9 u = 5.888... Which can be approximated to u ≈ 5.89. Thus, the final value for u is approximately 5.89.