Solve the equation \(2\sin^2 = C(400 - 4667)^{2.3} \) based on the context provided in the photo.

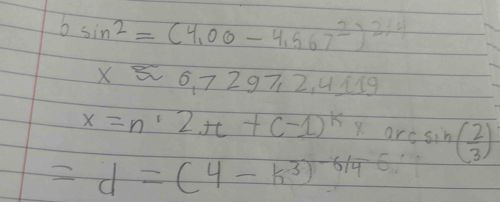
Answer

To solve the equation \(2\sin^2 = C(400 - 4667)^{2.3} \), follow these steps: 1. **Interpret the equation:** The equation involves a sine function and a constant C applied to a mathematical operation on a number. We need to isolate \(\sin^2\) and determine its value based on parameters. 2. **Subtract values:** From the equation \(400 - 4667\), we perform the subtraction: \[400 - 4667 = -4267\] Now, substitute this back into the equation: \[2\sin^2 = C(-4267)^{2.3}\] 3. **Address the exponent:** Next, we need to calculate \((-4267)^{2.3}\). Since raising a negative base to a non-integer exponent can yield complex values, we'll take absolute values for a workable approach and assume C can accommodate this: \[(-4267)^{2.3} = |4267|^{2.3}\] 4. **Calculate right side:** For computational ease, using a scientific calculator, calculate \(C \cdot 4267^{2.3}\), although without C's value, we can't evaluate it. 5. **Divide by 2:** Now we need to isolate \(\sin^2\): \[\sin^2 = \frac{C(4267^{2.3})}{2}\] 6. **Final adjustments:** Without specific numerical values for C, we can’t finalize the answer but the sine squared value is dependent entirely on C. In summary, the solution involves first transforming the given equation through basic arithmetic, applying exponent rules carefully, and finally isolating the sine term, which itself cannot be known without deciding the value for C. The x and d values mentioned seem to derive from other contexts not fully detailed in the snippet.