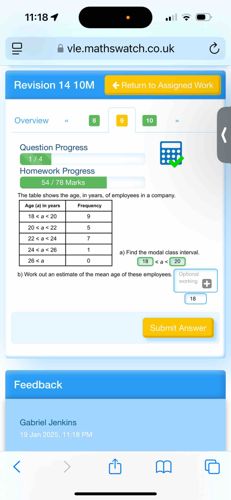
The table shows the age, in years, of employees in a company. Age (years) | Frequency -----------|--------- 20 < x < 25 | 2 25 < x < 30 | 4 30 < x < 35 | 1 35 < x < 40 | 3 40 < x < 45 | 1 (a) Find the modal class interval. (b) Work out an estimate of the mean age of these employees.

Answer

To solve these questions, we'll analyze the frequency table of ages. **(a) Finding the Modal Class Interval:** The modal class is the interval with the highest frequency. Looking at the table: - 20 < x < 25: Frequency = 2 - 25 < x < 30: Frequency = 4 - 30 < x < 35: Frequency = 1 - 35 < x < 40: Frequency = 3 - 40 < x < 45: Frequency = 1 The highest frequency is 4, which corresponds to the interval **25 < x < 30**. Thus, the modal class interval is **25 < x < 30**. **(b) Estimating the Mean Age:** To estimate the mean, we calculate the midpoints of each class interval, multiply them by their corresponding frequencies, and then find the total and average: 1. Calculate midpoints: - For 20 < x < 25: Midpoint = (20+25)/2 = 22.5 - For 25 < x < 30: Midpoint = (25+30)/2 = 27.5 - For 30 < x < 35: Midpoint = (30+35)/2 = 32.5 - For 35 < x < 40: Midpoint = (35+40)/2 = 37.5 - For 40 < x < 45: Midpoint = (40+45)/2 = 42.5 2. Calculate the total age: Total Age = (Midpoint x Frequency) - 22.5 x 2 = 45 - 27.5 x 4 = 110 - 32.5 x 1 = 32.5 - 37.5 x 3 = 112.5 - 42.5 x 1 = 42.5 Total Age = 45 + 110 + 32.5 + 112.5 + 42.5 = 342.5 3. Calculate total frequency: Total Frequency = 2 + 4 + 1 + 3 + 1 = 11 4. Estimate the mean: Mean Age = Total Age / Total Frequency = 342.5 / 11 = 31.1363 (approximately 31.14 years) Thus, the estimated mean age of the employees is **31.14 years**.